If you are currently studying for the GRE, you know that you have to learn a lot of information to get a great score. To learn so much material, you must follow a smart study plan that allows for topical learning and practice. Another part of your success will be developing tangible GRE quantitative strategies. They will help you navigate the rigors of GRE quant and make your test-day attack effective and efficient. So, in this article, we’ll provide plenty of GRE quant strategy, tips, and tricks and advice on how to study for the GRE math section.
GRE quant tests you on a variety of topics, so it is important to use every bit of advice you can get, so that your score will be as high as possible.
Here Are the Topics We’ll Cover:
To start, let’s discuss using smart numbers in certain quant problems.
Tip #1: Use Smart Numbers If Possible
If you have been studying for the GRE for any period of time, you likely have come across the term “smart numbers,” one of many GRE math strategies we’ll discuss in this article. Smart numbers are real numbers that you choose that make doing necessary calculations as simple as possible in a given problem.
For example, let’s say you need to determine what percent the final price of an item was of the original price, if the original price was first increased by 20 percent, and then decreased by 40 percent. To easily get through this question, we use the “smart number” of 100 for the original price, and then we calculate as follows:
The increase of 20 percent yields: 100 x 1.2 = 120
The decrease of 40 percent yields: 120 x 0.6 = 72
Thus, the new price is 72/100 x 100 = 72 percent of the original.
We see that by using a “smart number” of 100, we easily came up with the correct answer of 72 percent.

 KEY FACT:
KEY FACT:
Smart numbers are real numbers that you choose that make doing necessary calculations as simple as possible in a given problem.
When to Use Smart Numbers
Using smart numbers is generally ideal when dealing with a GRE question that requires you to work with fractions, ratios, or percentages. You can also use smart numbers in other types of questions, so this skill is one you’ll want to master!
The alternative to using smart numbers would be using variables, which is perfectly acceptable. However, using variables can create messy, timing-consuming math. With that in mind, we always have to be sure that the smart number we use instead makes sense and allows our math to be easier rather than more complicated.

 TTP PRO TIP:
TTP PRO TIP:
Use smart numbers to solve certain GRE math questions, such as those involving fractions, ratios, or percentages, for which you would otherwise use variables.
Let’s take a look at another use of smart numbers, this time in a problem that presents fractions.
Smart Number: Example 1
A certain animal shelter has only cats and dogs. At the shelter, 2/5 of the animals are cats, 1/8 of the animals are vaccinated, and 1/2 of the animals are dogs that are not vaccinated. What proportion of the dogs are vaccinated?
Solution:
We could let x = the total number of animals at the shelter. This would be a huge mistake! Why? Because all of our succeeding calculations would involve fractions and, worse, fractions of fractions.
Let’s avoid this mess by using the “smart number” of 40 to represent the total number of animals at the shelter. Why 40? Because it is the lowest common denominator (LCD) of the fractions mentioned in the problem. Let’s see how easy our math becomes if we use this smart number.
The number of cats at the shelter is (2/5)(40) = 16. Thus, the number of dogs is 40 – 16 = 24.
Now, half of the animals (half of 40 = 20) are unvaccinated dogs. This leaves 24 – 20 = 4 dogs that are vaccinated. Finally, to answer the question, we have 4 vaccinated dogs out of a total of 24 dogs, for a proportion of 4/24 = 1/6.
Using the smart number 40, which is the LCD of the fractions, turned a confusing problem into a rather easy one.
Answer: B
Next, let’s discuss knowing when to use your calculator.
Tip #2: Make Your Calculator Your Friend, Not Your Enemy
Don’t delay getting familiar with the GRE calculator. The GRE calculator is an onscreen tool provided during your exam; you may not use your own calculator! The onscreen calculator looks like this:
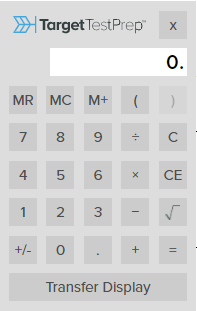
Whether you practice using the calculator on the ETS website when taking a practice test or in the TTP GRE self-study course, make sure you get plenty of practice using it before test day.

 TTP PRO TIP:
TTP PRO TIP:
Make sure that you are very familiar with the onscreen calculator before test day.
Now, let’s discuss when you should and should not use the calculator during your exam.
When to Use the Onscreen Calculator
When used properly, the GRE calculator can significantly benefit you. However, ETS (the folks who created the GRE) know you have access to the calculator, so they try their best to get you to use the GRE calculator when you don’t need to.
Let’s briefly look at some situations in which it makes sense to use the GRE calculator and when it makes sense not to use it.
Cases in which you should use the calculator:
- Unwieldy calculations, such as 1.0021 / 0.21 or 563 x 10,111
- Numbers raised to powers, such as 133^3 or 2^9
- Square roots of numbers that are not perfect squares, such as the square root of 111 or the square root of 65
Cases in which you should NOT use the calculator:
- Basic math, such as 8 x 12 or 6 + 4 + 3
- Simple fractions, such as 120 / 10 or even [(11 / 40) x (8 / 22)] (you can cancel and simplify)
- Basic square roots, such as the square root of 81 or the square root of 144.
Let’s now look at a few GRE math problems for which using math shortcuts or GRE math tricks is faster than using your calculator.
When Not to Use the Calculator: Example 1
6^8 is equal to which of the following?
- 1,676,558
- 1,678,661
- 1,679,616
- 1,670,037
- 1,671,284
Solution:
If you use the calculator to calculate 6 raised to the 8th power, you will obtain the correct answer. However, it will take 16 keystrokes to enter this problem into the calculator. Moreover, you are prone to making a miscount or keystroke error when entering 6 x 6 x 6 x 6 x 6 x 6 x 6 x 6 into the calculator.
So, instead of using the calculator, you should recall the rule that any number that ends in 6, when raised to a whole number power, will also end in 6. Thus, it’s clear that the answer is C, because C is the only answer choice that has a units (ones) digit of 6. No calculation necessary!
Answer: C
By following the rule described above, we answered this question in about 10 seconds, and we didn’t need to use the unwieldy, inconvenient calculator. Pretty cool, right?
Let’s try another example.
When Not to Use the Calculator: Example 2
Which of the following is equal to 12!?
- 423,734,164
- 438,309,883
- 445,622,291
- 452,550,728
- 479,001,600
Solution:
First, you need to recall that 12! (pronounced “12 factorial”) is the notation for repeated multiplication. And even if you know that 12! = 12 x 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1, you might be tempted to use the onscreen GRE calculator to get the answer. Big mistake! The calculator gives an error message! The answer is too large for the calculator display. So, what now?
At the outset of the problem, you should have recalled the rule that any factorial greater than 4! will have a units (ones) digit of 0. The only answer choice that ends in 0 is choice E.
Answer: E
We now see that, while the calculator can be a useful tool for the GRE, its utility is limited. There is no substitute for dedicated study and recognition of rules that we have studied and committed to memory.

 TTP PRO TIP:
TTP PRO TIP:
The onscreen GRE calculator is a useful tool, but it is sometimes inefficient to use.
Tip #3: Memorize QC Answer Choices and Understand What They Mean
The GRE quant section contains four major question types, and one of the more challenging types is Quantitative Comparison questions (QC). QC questions present two quantities, Quantity A and Quantity B. You must determine whether there is a consistent relationship between the two.
One great thing about Quantitative Comparison questions is that the answer choices are always the same. Thus, you’ll want to memorize these answer choices to save time answering these questions. Remember, every second counts! The answer choices are as follows:


 TTP PRO TIP:
TTP PRO TIP:
Memorize the QC answer choices!
Understand How to Interpret the Answer Choices
You need to ensure that you understand what each of the QC answer choices indicates. For example, answer choice A — Quantity A is greater than Quantity B — actually means that Quantity A is ALWAYS greater than Quantity B.
For example, if you are given that Quantity A is 58 and Quantity B is 33, then it is obvious that Quantity A is always greater than Quantity B, since 58 is always greater than 33. You would confidently choose answer choice A.
Let’s take a look at an additional example question.
QC Answer Choices: Example 1
Quantity A:
x
Quantity B:
33
Solution:
Since x is a variable, we must plug in all possible types of values for x. For example, if we let x = 91, then quantity A is greater than quantity B. But you can’t stop there!
We could also let x = 0, and then quantity B is greater than quantity A. And if we let x = -3, then quantity B is greater than quantity A. Furthermore, if we let x = 33, then quantities A and B are equal.
So, since there is not a consistent relationship between the two quantities, we would choose answer D — the relationship between the two quantities cannot be determined.
Answer: D

 TTP PRO TIP:
TTP PRO TIP:
When a variable is involved in a QC question, we must consider all possible types of values that the variable can take on.
Now, let’s discuss another useful tip related to QC questions: making sure to use all given information when evaluating the quantities.
Tip #4: Consider All Given Information in QC Questions
You may notice in Quantitative Comparison questions that sometimes there is “given information” in the question stem. The “given information” is critical, especially when it contains qualifiers. Qualifiers include descriptions such as x > 0, x is a positive integer, or y is an even number.
A qualifier may whittle down your possible answer choices, but unfortunately it is easy to skip over if you are not careful. Remember though, missing any given information could be the difference between an incorrect and a correct answer.
For example, let’s say you had a QC question with given information but no qualifiers in the question stem:
Given: x² – 2x – 15 = 0
Quantity A: x
Quantity B: 2
Simplifying the question stem, we have the following:
x² – 2x – 15 = 0
(x – 5)(x + 3) = 0
x = 5 or x = -3
When x = 5, quantity A is greater than quantity B. But when x = -3, quantity A is less than quantity B. Since we have possible values for x greater than and less than 2, we have an inconsistent relationship between the quantities. Therefore, the answer is D.
Now, let’s look at the identical problem with one small change: qualifying information is given in the question stem.
Given: x > 0 and x² – 2x – 15 = 0
Quantity A: x
Quantity B: 2
Simplifying the question stem, we have the following:
x² – 2x – 15 = 0
(x – 5)(x + 3) = 0
x = 5 or x = -3
Since the qualifying information in the question stem tells us that x is greater than zero, x = 5 is the only valid value of x, and thus quantity A is greater than quantity B. Notice how the qualifier x > 0 changed the answer!

 TTP PRO TIP:
TTP PRO TIP:
Read and consider all given information in QC questions.
Let’s now work through an example.
QC Qualifying Information: Example 1
x is a nonzero integer.
Quantity A:
x
Quantity B:
1/4
Solution:
First, we note that quantity A will always be positive because any nonzero number that is squared is positive. If we choose positive integers for x, such as 1, 2, 3, etc., we see that x2 is greater than 1/4. And if we choose negative integers, such as -1, -2, -3, etc., then x2 is also greater than 1/4. Thus, we see that A is the correct answer.
If we hadn’t paid attention to the qualifying information in the question stem, we might carelessly have chosen a value such as x = 1/2, which would make the two quantities equal, or values such as x = 1/3 or 1/4, which would make quantity B greater than quantity A. This mistake would have led us to the trap answer of D.
The qualifier provided the valuable information that x is a nonzero integer, which means that x can be any whole number except 0. Choosing appropriate values of x to satisfy that qualifier allowed us to arrive at the correct answer easily.
Answer: A
Our next tip is to recognize the significance of the phrase “closest to” in GRE quant questions.
Tip #5: The Phrase “Closest to” Is Meaningful in GRE Quant Questions
As we have already discussed, it’s important to be mindful of all information provided in GRE quant questions, regardless of how insignificant that information may seem. Case in point: the phrase “closest to.” This is an important phrase because it implies that we can rely on estimation to come up with an answer. If we miss this information in a question, we may take the question much farther than it needs to go to come up with an answer.
For example, let’s say we need to know which of the following answer choices is closest to 28^18 – 7^9.
A. 28^18
B. 28^17
C. 28^16
D. 28^15
E. 28^14
First, don’t even think about trying this on the calculator! And don’t try re-expressing the bases of 28 and 7 to primes, which although correct mathematically, is unnecessary. Return to the question stem and notice the phrase “closest to,” which is a big hint that very little math, if any, is needed to solve this problem. To get the correct answer, we must recognize that because 28^18 is so much bigger than 7^9, the approximate answer is still 28^18. So, by recognizing the words “closest to,” we can solve this question in seconds rather than minutes.

 TTP PRO TIP:
TTP PRO TIP:
Pay attention to the phrase “closest to” in a question stem; when you see it, be sure to use approximation.
Let’s try another example.
“Closest to”: Example 1
(20,103 x 1,025) / (19 x 57) is closest to which of the following?
- 200
- 2,000
- 20,000
- 200,000
- 2,000,000
Solution:
Our initial reaction to this question may be to use the onscreen calculator to find the exact value of the given expression and determine the answer choice that is closest to the result. While that approach is not wrong, it is a waste of time. Instead, we should notice that the answer choices are spaced far enough for us to easily determine the correct answer using estimation.
If we approximate 20,103 as 20,000, 1,025 as 1,000, 19 as 20, and 57 as 50, the expression becomes the following:
(20,103 x 1,025) / (19 x 57) = (20,000 x 1,000) / (20 x 50) = 20,000
Thus, we can conclude with confidence that the given expression is closest to 20,000. We can compare this answer to the value we would obtain if we used the calculator. Carrying out the given operations, we would obtain 19,026.39, which is pretty close to the approximate value we found. By using estimation, however, we were able to save valuable time.
Answer: C
Tip #6: Memorize Essential Quant Formulas
As you know, the GRE is a timed exam, meaning that when you’re attacking problems, every second counts! A great way to save time on GRE quant is to memorize as many formulas, concepts, and procedures as possible. I can’t stress enough how important memorization is as one of your main problem-solving strategies.
For example, if you see an average rate question, you need to quickly utilize the formula average rate = (total distance)/(total time). Or, if you see a question involving the difference of squares, you need to be able to quickly use the formula (x + y)(x – y) = x^2 – y^2. These are just a couple of examples, but I think you get the point!
A great way to memorize all of these formulas is to create a set of flashcards. Essentially, whenever you come across a formula you think you should know, put it on a flashcard! That way, by test day, you won’t need to waste time trying to recall a needed formula.
Let’s practice a few questions to illustrate the importance of this memorization. When reading through the solutions, I want you to think about how much time you save on these questions by memorizing certain concepts or formulas.

 TTP PRO TIP:
TTP PRO TIP:
The more formulas you know, the faster and more confident you will be when answering GRE quant questions.
Memorized Facts: Example 1
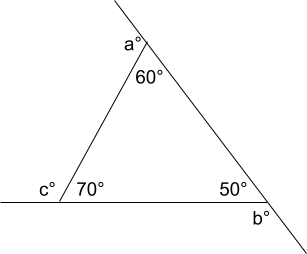
In the figure above, what is the value of a + b + c?
- 180°
- 220°
- 260°
- 300°
- 360°
Solution:
There are two ways to solve this question: the short way and the long way.
The short way results from your having memorized that the sum of the exterior angles of a polygon is 360 degrees. Answer E is correct.
The long way requires that you calculate the individual values of angles a, b, and c, using the fact that a straight angle measures 180 degrees, as follows:
a = 180 – 60 = 120
b = 180 – 50 = 130
c = 180 – 70 = 110
Thus, a + b + c = 120 + 130 + 110 = 360.
If you memorized the fact about the sum of exterior angles of a polygon, you saved yourself a minute or more of time, which you can use later to solve a more challenging problem.
Answer: E
Let’s take a look at another example showing the importance of memorizing math facts and concepts.
Memorized Facts: Example 2
Quantity A:
23% of 11,459
Quantity B:
11,459% of 23
Solution:
Again, there are two ways to solve this problem: the short way and the long way.
The short way results from your having memorized that a% of b is equal to b% of a. For example, 10% of 50 is equal to 50% of 10. In each case, the answer is 5.
For this question, we use the above math fact, and we find that the two quantities are equal. Note that it is not necessary to make any calculations. The correct answer is C.
The long way requires the use of the slow and cumbersome online calculator, as follows:
23% of 11,459 = 0.23 x 11,459 = 2,635.57
11,459% x 23 = 114.59 x 23 = 2,635.57
Try the long way using the online GRE calculator, and you’ll see that the 21 keystrokes required to calculate the two answers take a significant number of seconds to complete!
Answer: B
Tip #7: Don’t “Game” Which Quant Questions Will Show Up
A question I am asked often is, “What are the quant topics that are most likely to appear on my GRE?” Unfortunately, any honest GRE professional will tell you that there is no way to know exactly what will show up on your exam. It does not matter if you have hyper-analyzed every official GRE practice test or even memorized what you saw on previous GREs. The fact is, every GRE is unique, and no one can tell you with certainty what will show up on any given exam.
So, rather than trying to game the system by predicting what you might see, get rock solid with all GRE quant topics, so that you won’t be spinning a roulette wheel on test day.
Remember, there are only 40 quant questions on the GRE (20 questions per section). Thus, you have just 40 opportunities for GRE quant success. So, if you decide to skip a couple of major GRE quant topics during your prep, and 10 questions on those topics show up, then you will be in a tough spot on test day.

 TTP PRO TIP:
TTP PRO TIP:
Don’t try to predict what GRE quant topics you’ll see on your exam.
Tip #8: Treat VIC Problems as You Would Any Other Quant Problem
“VIC” problems are a specific type of GRE quant problem. The term VIC refers to problems that have “Variables in (the answer) Choices.” Now, while VIC problems look more foreboding than garden-variety GRE quant questions, the math involved in a VIC problem does not differ from the math used when we have actual numbers. This idea is important because it means that when solving a VIC problem, you should do exactly what you would do if real numbers were involved.
In other words, you don’t have to replace the variables with actual numbers! Doing so would slow you down and increase the potential for mistakes.
Let’s look at two almost identical problems to understand what I mean.
Example 1 (Non-VIC)
Nitish and Goran have 14 baseball cards. If Nitish has 4 more baseball cards than Goran, how many cards does Goran have?
Solution:
We can let n = the number of cards Nitish has and g = the number of cards Goran has. We can create two equations:
n + g = 14
and
n = g + 4
Substituting g + 4 for n, we have:
g + 4 + g = 14
2g = 10
g = 5
Answer: C
Now, let’s look at the problem we just did as a VIC problem, with the answer choices containing variables instead of numbers. Keep a close eye on how the process of solving does not change.
Example 2 (VIC)
Nitish and Goran have x baseball cards. If Nitish has y more baseball cards than Goran, in terms of x and y, how many cards does Goran have?
- x – y
- y – x
- (x – y)/2
- (x – y)/4
- (x + y)/2
Solution:
We can let n = the number of cards Nitish has and g = the number of cards Goran has. Let’s now create two equations:
n + g = x
and
n = g + y
Substituting g + y for n, we have:
g + y + g = x
2g = x – y
g = (x – y)/2
Answer: C
Notice that we did not have to replace the variables with actual numbers because the process was the same in both problems!
Sure, we could have plugged in absolute numbers for x and y, but then we would have had to plug the values we chose for x and y back into the answer choices to find the correct answer. That would have taken time and potentially introduced any number of mistakes. If you can efficiently evaluate equations with just variables, you will save a lot of time and improve your accuracy on GRE quant.

 TTP PRO TIP:
TTP PRO TIP:
Don’t let VIC questions unnerve you. If you can solve a problem with numbers, then with a bit of practice, you can solve VIC questions just as easily!
Tip #9: Answer Every Question!
A great aspect of the GRE is that you can move back and forth between questions in a section. In other words, if you are unsure of an answer to a question, you can skip it, mark it for review, and return to it if you have time. However, you must understand that you are not penalized for wrong answers.
So, even if you don’t know the answer to a particular question and intend to return to the question, DON’T LEAVE IT BLANK! Here’s why: if you forget to come back to a question, or if you run out of time before you have a chance to revisit it, there is a 100 percent chance you’ll get it wrong if you leave it blank. However, if you take a guess, there’s a chance that your guess could be correct! So, the process is:
- Guess.
- Mark for review.
- Come back if you have time.

 TTP PRO TIP:
TTP PRO TIP:
Don’t leave any GRE quant question blank.
Guessing Strategies: Multiple Choice and QC Questions
Many students agonize over which answer choice to guess. If you are randomly guessing, just pick any answer choice and move on. There is no answer choice that is more advantageous than any other. So, before the exam, decide which oval you will use as your “guess” oval. Don’t waste time during the exam stressing over which one to choose, knowing you have no idea. Just guess and move on.
A caution: Many students stumped on a Quantitative Comparison question tend to choose D as their guess. They think that if they don’t know the answer, then choosing D, “The relationship between the two quantities cannot be determined,” is the best choice. Before you resort to choice D, ensure that you have given the question a fair shake. Just because YOU can’t determine the relationship between the two quantities doesn’t mean that D is the correct answer.
Now, if you can eliminate any answer choice, great! Your probability of getting the question correct increases significantly for each answer choice you can eliminate. So, give every question a solid attempt before resorting to guessing.

 TTP PRO TIP:
TTP PRO TIP:
Give every question a solid attempt before resorting to guessing.
What About Numeric Entry Questions?
The same basic guessing strategy applies even to numeric entry (fill-in-the-blank) questions. Even though you can’t eliminate any answer choices because there are none, you can still make sure to enter an answer into the box. Granted, you have a small chance of landing on a lucky guess, but hey, there is no penalty for an incorrect answer, so go for it!
Here are a few tips for numeric entry question guessing;
If you have to guess randomly, enter a “reasonable” number. Get a feel for what might be a good guess. If the question asks “how many,” a good guess might be a number between, say, 5 and 20. If a fraction is asked for, guess a common fraction, such as ½ or ¾. Enter a negative number if you need to determine the smallest root of a tough algebra problem.
Remember, guessing is just one component of the GRE math time-management strategy you want to perfect before test day.
Tip #10: Don’t Double-Check Your Work
Far too often, I have spoken with students after a failed GRE test who have mentioned that they ran out of time. However, their explanation was not that they did not know the material or had test anxiety. It was that they double-checked their work! Remember, you have an average of only one minute and 45 seconds for each GRE math question. Many questions will take you at least that long, and some will take longer. So, as you can imagine, you won’t have time left to check your work. If you finish a question quickly, you’ll want to “bank that time” to use on a later problem that may take you longer than 1:45 to complete.

 TTP PRO TIP:
TTP PRO TIP:
You don’t have time to double-check your work on the GRE.
Summary: Top 10 GRE Quant Strategies for a Top Score
We have covered a lot of territory in this article! GRE quant is not easy, so every tip you know and follow will help you earn your best score possible. Let’s take a look at the 10 GRE Math tips and tricks that we have covered here:
- Use smart numbers when possible.
- Make your calculator your friend, not your enemy.
- Memorize QC answer choices and understand what they mean.
- Consider all given information in QC questions.
- The phrase “closest to” is meaningful in GRE quant questions.
- Memorize essential quant formulas.
- Don’t “game” which quant questions will show up.
- Treat “VIC” problems as you would any other quant problem.
- Answer every question!
- Don’t double-check your work.
Frequently Asked Questions (FAQ)
How Can I Improve My Math Score on the GRE?
While GRE quant is not a walk in the park, it is quite possible to earn a respectable score. The key is commitment. Create a solid study plan, stick with it, and do everything necessary to be successful on the exam. The tips provided in this article will help you tremendously in reaching your goal.
How Hard Is It to Get 170 on the GRE?
A GRE quant score of 170 is in the 96th percentile, and a GRE verbal score of 170 is in the 99th percentile. So, very few individuals earn these stratospheric scores. Those who do have most likely spent a significant amount of time preparing for the GRE. While you might not get a perfect score on the GRE, you can definitely earn a great score with committed preparation and great study resources.
What’s Next?
GRE quant tests you on a variety of topics, so it is important to use every bit of advice you can get, so that your score will be as high as possible.
If you follow the tips presented in this article, you will definitely get a boost to your GRE math prep. Once you have made inroads in your quant studying, you might need some help in getting faster at answering GRE quant questions. Follow the suggestions in that article to improve your speed, and you’ll be closer to your target score than ever before.
Good luck!




