In Euclidean geometry, a quadrilateral is a four-sided 2D figure whose sum of internal angles is 360°. The word quadrilateral is derived from two Latin words ‘quadri’ and ‘latus’ meaning four and side respectively. Therefore, identifying the properties of quadrilaterals is important when trying to distinguish them from other polygons. So, what are the properties of quadrilaterals? There are two properties of quadrilaterals:
- A quadrilateral should be closed shape with 4 sides
- All the internal angles of a quadrilateral sum up to 360°
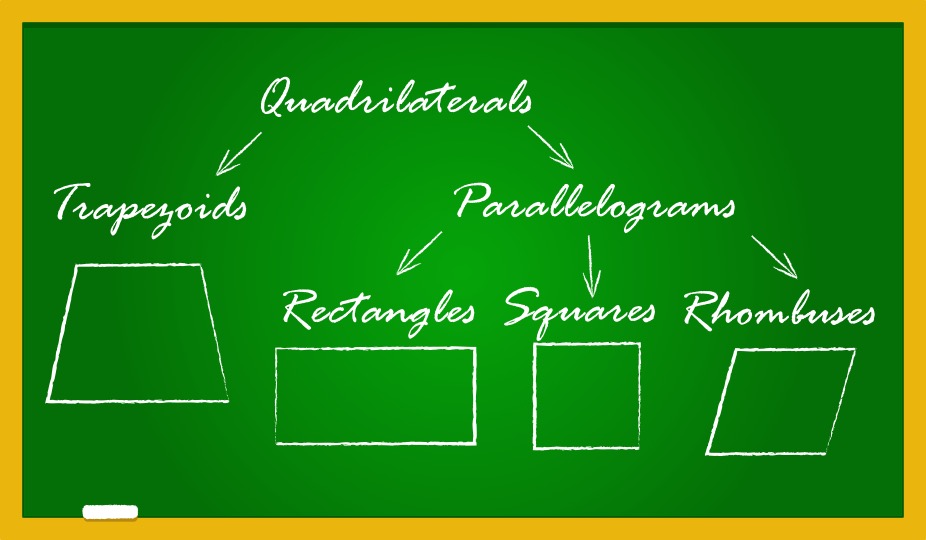
In this article, you will get an idea about the 5 types of quadrilaterals (Rectangle, Square, Parallelogram, Rhombus, and Trapezium) and get to know about the properties of quadrilaterals.
Here are the five types of quadrilaterals discussed in this article:
- Rectangle
- Square
- Parallelogram
- Rhombus
- Trapezium
Are you struggling with GMAT quant? e-GMAT provides structured learning from foundations to help you master the skills needed for a high score. Join the world’s most successful prep company for a free trial and see the difference it can make. We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub, as of March 2023.
Here is a video explaining the properties of quadrilaterals:
Properties of the quadrilaterals – An overview
The diagram given below shows a quadrilateral ABCD and the sum of its internal angles. All the internal angles sum up to 360°. Thus, ∠A + ∠B + ∠C + ∠D = 360°
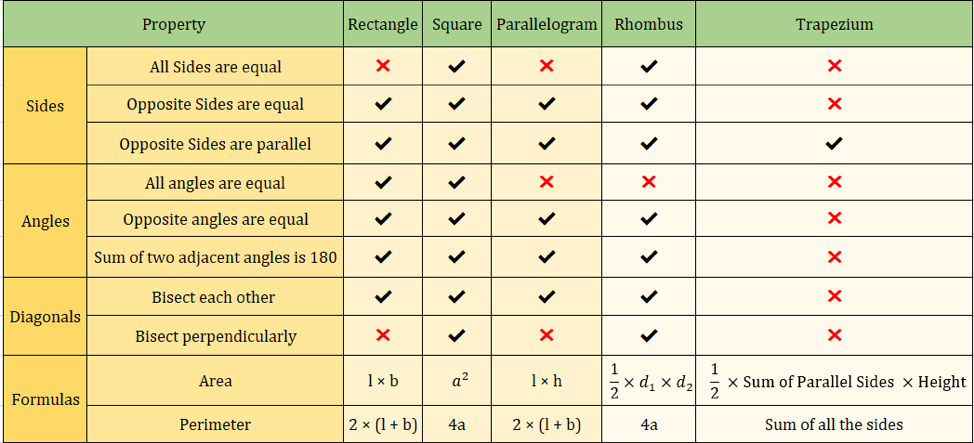
| Properties of quadrilaterals | Rectangle | Square | Parallelogram | Rhombus | Trapezium |
| All Sides are equal | No | Yes | No | Yes | No |
| Opposite Sides are equal | Yes | Yes | Yes | Yes | No |
| Opposite Sides are parallel | Yes | Yes | Yes | Yes | Yes |
| All angles are equal | Yes | Yes | No | No | No |
| Opposite angles are equal | Yes | Yes | Yes | Yes | No |
| Sum of two adjacent angles is 180 | Yes | Yes | Yes | Yes | No |
| Bisect each other | Yes | Yes | Yes | Yes | No |
| Bisect perpendicularly | No | Yes | No | Yes | No |
Let’s discuss each of these 5 quadrilaterals in detail:
Rectangle
A rectangle is a quadrilateral with four right angles. Thus, all the angles in a rectangle are equal (360°/4 = 90°). Moreover, the opposite sides of a rectangle are parallel and equal, and diagonals bisect each other.
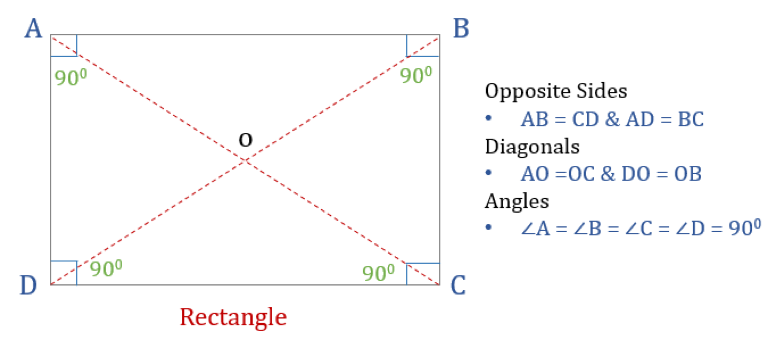
Here are the three properties of a rectangle:
- All the angles of a rectangle are 90°
- Opposite sides of a rectangle are equal and Parallel
- Diagonals of a rectangle bisect each other
Rectangle formula – area and perimeter of a rectangle
If the length of the rectangle is L and breadth is B then,
- Area of a rectangle = Length × Breadth or L × B
- Perimeter of rectangle = 2 × (L + B)
These practice questions will help you solidify the properties of rectangles
Are you struggling with GMAT quant? e-GMAT provides structured learning from foundations to help you master the skills needed for a high score. Join the world’s most successful prep company for a free trial and see the difference it can make. We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub, as of April 2023.
Did you know e-GMATers have reported more 700+ scores than ever before in GMAT Club’s history? Watch this video to understand how e-GMAT has achieved this record-shattering result by investing and innovating with a single goal in mind – To create a platform that empowers students to achieve and deliver their very best.
Square
Square is a quadrilateral with four equal sides and angles. It’s also a regular quadrilateral as both its sides and angles are equal. Just like a rectangle, a square has four angles of 90° each. It can also be seen as a rectangle whose two adjacent sides are equal.
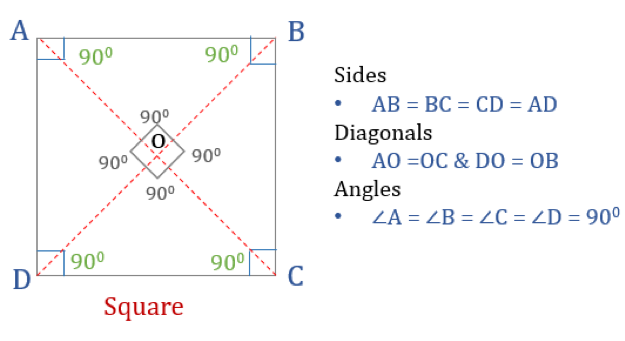
Here are the three properties of a Square:
- All the angles of a square are 90°
- All sides of a square are equal and parallel to each other
- Diagonals bisect each other perpendicularly
Square formula – area and perimeter of a square
If the side of a square is ‘a’ then,
- Area of the square = a × a = a²
- Perimeter of the square = 2 × (a + a) = 4a
These practice questions will help you solidify the properties of squares
Scoring a Q50-51 on the GMAT helps you get a 700+ GMAT score. Start your journey of getting a Q50-51 on the GMAT with e-GMAT’s AI-driven online preparation course. Our xPERT not only curates the most optimized learning path but also tracks your improvement, ensuring that you get to your target Quant score quickly and reliably. Watch this video to know more:
Parallelogram
A parallelogram, as the name suggests, is a simple quadrilateral whose opposite sides are parallel. Thus, it has two pairs of parallel sides. Moreover, the opposite angles in a parallelogram are equal and their diagonals bisect each other.
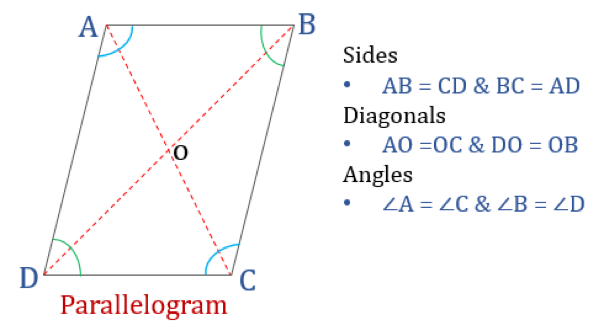
Here are the four properties of a Parallelogram:
- Opposite angles are equal
- Opposite sides are equal and parallel
- Diagonals bisect each other
- Sum of any two adjacent angles is 180°
Parallelogram formulas – area and perimeter of a parallelogram
If the length of a parallelogram is ‘l’, breadth is ‘b’ and height is ‘h’ then:
- Perimeter of parallelogram= 2 × (l + b)
- Area of the parallelogram = l × h
These practice questions will help you solidify the properties of parallelogram
Rhombus
A rhombus is a quadrilateral whose all four sides are equal in length and opposite sides are parallel to each other. However, the angles are not equal to 90°. A rhombus with right angles would become a square. Another name for rhombus is ‘diamond’ as it looks similar to the diamond suit in playing cards.
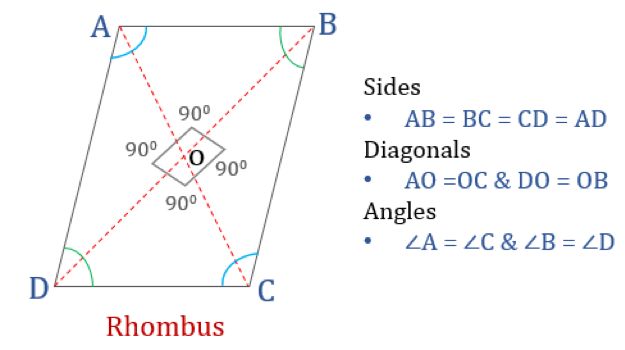
Here are the four properties of a Rhombus:
- Opposite angles are equal
- All sides are equal and, opposite sides are parallel to each other
- Diagonals bisect each other perpendicularly
- Sum of any two adjacent angles is 180°
Rhombus formulas – area and perimeter of a rhombus
If the side of a rhombus is a then, perimeter of a rhombus = 4a
If the length of two diagonals of the rhombus is d1 and d2 then the area of a rhombus = ½ × d1 × d2
These practice questions will help you solidify the properties of rhombus
Trapezium
A trapezium (called Trapezoid in the US) is a quadrilateral that has only one pair of parallel sides. The parallel sides are referred to as ‘bases’ and the other two sides are called ‘legs’ or lateral sides.
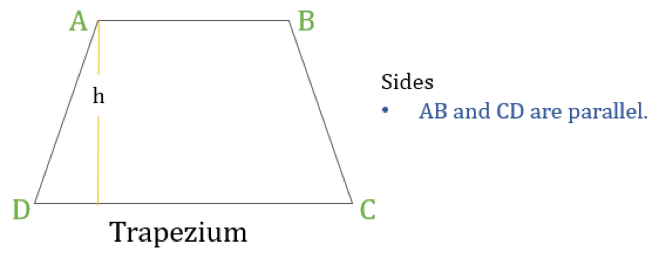
A trapezium is a quadrilateral in which the following one property:
- Only one pair of opposite sides are parallel to each other
Trapezium formulas – area and perimeter of a trapezium
If the height of a trapezium is ‘h’ (as shown in the above diagram) then:
- Perimeter of the trapezium= Sum of lengths of all the sides = AB + BC + CD + DA
- Area of the trapezium = ½ × (Sum of lengths of parallel sides) × h = ½ × (AB + CD) × h
These practice questions will help you solidify the properties of trapezium
Properties of Quadrilaterals – Summary
The below image also summarizes the properties of quadrilaterals
Are you struggling with GMAT quant? e-GMAT provides structured learning from foundations to help you master the skills needed for a high score. Join the world’s most successful prep company for a free trial and see the difference it can make. We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub, as of April 2023.
Important quadrilateral formulas
The below table summarizes the formulas on the area and perimeter of different types of quadrilaterals:
| Quadrilateral formulas | Rectangle | Square | Parallelogram | Rhombus | Trapezium |
| Area | l × b | a² | l × h | ½ × d1 × d2 | ½ × (Sum of parallel sides) × height |
| Perimeter | 2 × (l + b) | 4a | 2 × (l + b) | 4a | Sum of all the sides |
Further reading:
To ace the GMAT a well-defined study plan is required. Save 60+ hours on GMAT preparation by following these three steps:
Quadrilateral Practice Question
Let’s practice the application of properties of quadrilaterals on the following sample questions:
GMAT Quadrilaterials Practice Question 1
Adam wants to build a fence around his rectangular garden of length 10 meters and width 15 meters. How many meters of fence he should buy to fence the entire garden?
- 20 meters
- 25 meters
- 30 meters
- 40 meters
- 50 meters
Solution
Step 1: Given
- Adam has a rectangular garden.
- It has a length of 10 meters and a width of 15 meters.
- He wants to build a fence around it.
Step 2: To find
- The length required to build the fence around the entire garden.
Step 3: Approach and Working out
The fence can only be built around the outside sides of the garden.
- So, the total length of the fence required= Sum of lengths of all the sides of the garden.
- Since the garden is rectangular, the sum of the length of all the sides is nothing but the perimeter of the garden.
- Perimeter = 2 × (10 + 15) = 50 metres
Hence, the required length of the fence is 50 meters.
Therefore, option E is the correct answer.
GMAT Quadrilaterals Practice Question 2
Steve wants to paint one rectangular-shaped wall of his room. The cost to paint the wall is $1.5 per square meter. If the wall is 25 meters long and 18 meters wide, then what is the total cost to paint the wall?
- $ 300
- $ 350
- $ 450
- $ 600
- $ 675
Solution
Step 1: Given
- Steve wants to paint one wall of his room.
- The wall is 25 meters long and 18 meters wide.
- Cost to paint the wall is $1.5 per square meter.
Step 2: To find
- The total cost to paint the wall.
Step 3: Approach and Working out
- A wall is painted across its entire area.
- So, if we find the total area of the wall in square meters and multiply it by the cost to paint 1 square meter of the wall then we can the total cost.
- Area of the wall = length × Breadth = 25 metres × 18 metres = 450 square metre
- Total cost to paint the wall = 450 × $1.5 = $675
Hence, the correct answer is option E.
We hope by now you would have learned the different types of quadrilaterals, their properties, and formulas and how to apply these concepts to solve questions on quadrilaterals. The application of quadrilaterals is important to solve geometry questions on the GMAT. If you are planning to take the GMAT, we can help you with high-quality study material which you can access for free by registering here.
Here are a few more articles on Math:
- Improve accuracy in Math questions on Polygons
- Geometry Questions – Most Common Mistakes | GMAT Quant Prep
Watch this GMAT geometry-free webinar where we discuss how to solve 700-level Data sufficiency and Problem questions in GMAT Quadrilaterals:
Are you planning to enroll at top business schools? Let us help you conquer the first step of the process i.e., taking the GMAT. Take a free GMAT mock to understand your baseline score and start your GMAT prep with our free trial. We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub, as of January 2023.
Write to us at acethegmat@e-gmat.com in case of any query.
FAQs
There are 5 types of quadrilaterals – Rectangle, Square, Parallelogram, Trapezium or Trapezoid, and Rhombus.
You can find a few practice questions on quadrilaterals in this article.
The sum of interior angles of a quadrilateral is 360°.